確率は、中学入試・高校受入試・大学入試のすべてで出題されます。さまざまな難度の問題を比較的容易に作成でき、数学的思考力を試せることが一因です。入試問題の難易度は概ね次の通りです。
(公立中学の定期試験<)公立高校<中堅私立中学<難関私立中学=中堅私立大学<難関私立大学(≒難関私立中学)<難関国立大学
※ 難関私立中学の定期試験の問題は、難関私立大学入試問題のレベルに到達しています。
公立高校の確率の入試問題例
<<解法のポイント>>
解法はワンパターンで簡単で、お決まりの6X6のマスを作り、
1.大(a)・小(b)のさいころの和が4、7、10になるものを数え上げればよい。
※和が1になるものは存在しないので、対象外。
2.大(a)・小(b)のさいころの和が5、8、11になるものの中で、aがbの約数にならないものを数え上げればよい。
※和が2になるものはa=1がb=1の約数になるので対象外。
私立中学(女子校)の場合の数の入試問題例
※ 合格率80%偏差値60台(サピックス)の中学入試問題です。
※ 男子校の算数はさらに難度が上がります。
中学入試では柔軟な思考力が要求されますので、公立高校入試の単純な思考で解ける問題しか解いていないと、ほとんど解けません。
<<解法のポイント>>
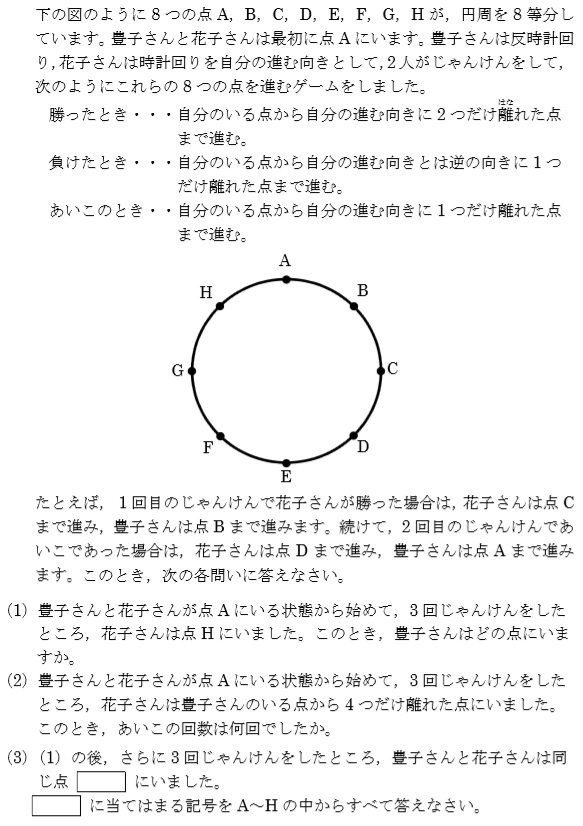
時計回りを正とし、反時計回りを負として、整理すると解き易くなります。
勝ちを〇、あいこを△、負けを✖と記号化すればさらに思考が楽になります。
花子 勝ち あいこ 負け +2 +1 -1
豊子 負け あいこ 勝ち +1 -1 -2
1.3回で花子がー1になる組み合わせは△✖✖であるから、豊子は△〇〇=-1-2-2=-5
2.”花子ー豊子”を求めて、差が4になるものを求めればよい。
花子ー豊子は、+1 +2 +1となり、3回で+4となるのは△一回とわかる。
3.差が4となる組み合わせを求めればよい。花子に着目すると△〇〇=+5、△〇✖=+2、△✖✖=-1の3通り。
私立大学(理系)の確率の入試問題例
※ 合格率80%以上偏差値60(2019年度6月実施の第1回駿台全国模試でA判定)
※ 私立最難関大学の最難関学部の問題(医学部を除く)
※ 私立大学の入試問題は難関大学でも、具体的で解き易い傾向があります。
<<解法のポイント>>
3n回以内にAが勝つのは、次のn通りである。
2+3✕0回目 AA
2+3✕1回目 ACBAA
2+3✕2回目 ACBACBAA
・・・
2+3✕(n-1)回目 ACBACB・・・ACBAA
よって、求める確率は初項が1/4、公比が1/8の等比数列の和である。

難関私立中学(2年3学期~3年1学期)の確率の定期試験の問題例(改)
※ この問題は、私立の難関大学入試問題に匹敵するレベルに到達しています。
※ 合格率80%偏差値60超え(サピックス)の中学の定期試験レベルの問題で、中学生でこの問題を自力で解けるなら東大合格の素質があります。
中学受験で難関中学入学を目指すご家庭は、合格しても、大学に合格するまで気の休まるときは無いことを覚悟しておくことです。さらに、大学に合格しても東大クラスだと大学でも勉強漬けの日々が待っています。
このレベルの中学生を指導できる塾は、極めて少なく、(当塾は例外ですが)一般的に高額であることも覚悟しておくことです。
最近、大手塾に通っていた私立(合格率80%偏差値50台:サピックス)の中学生が、その塾では手にあまり指導できないことに(漸く)気づき、当塾に入塾しましたが、このレベルでも高校生になると、満足な指導を受けられる塾は、さらに少なくなります。
※ 中学受験の合格率80%偏差値(サピックス)
開成(67)、聖光学院(64)、栄光学園(62)、慶応(58)、浅野(57)、逗子開成(51)、鎌倉学園(50)、フェリス女学院(56)、湘南白百合(50未満)
※ 高校受験の合格率80%偏差値(サピックス)
日比谷(58)、横浜翠嵐(55)、湘南(54)、柏陽(48)、厚木(44)
<<解法のポイント>>
1.出る目が1以外となる組み合わせは、次の3通り。
2が3回(2、2、2)、2が一回出てかつ3が1回(2、3)4が1回(4)。
これらの場合の数は、それぞれ、nC3、nP2、nP1通りである。
さいころn個を同時に投げるときの一回当たりの確率はそれぞれ(1/6)^nであるから、
求める確率は(nC3+nP2+nP1)✕(1/6)^nである。
2.3種類の解法を紹介します。
解法1.8回目で初めて0になるのは、4回目・6回目が共に0にならず8回目が0になるときである。
6回目で0にならず8回目で0になるのは、6回目の得点が2点で、7回目・8回目が共に裏がでるときである。
6回投げて4回目で0にならず6回目の得点が2になる確率は、6回目で2点になるのは表が2回・裏が4回でるときであり、4回目で0になるのは4回すべてが裏のときであることより、(6C2-1)(1/2)^6である。
7回・8回の2回投げて2回共に裏がでる確率は(1/2)^2である。
以上より、求める確率は(6C2-1)(1/2)^6(1/2)^2 となる。
解法2.求める確率は、8回目の持ち点が0となる確率から、4回目・8回目が0、6回目・8回目が0となる確率を引き、4回目・6回目・8回目が0となる確率を加えればよい。
8回投げて8回目が0になるのは、表が2回、裏が6回でるときである。
このときの確率は、8C2(1/2)^6・(1/2)^2=8C2(1/2)^8 ・・・①
4回目0・8回目0となる確率は、4C4(1/2)^4・4C2(1/2)^4 =6(1/2)^8 ・・・②
6回目0・8回目0となる確率は、6C1(1/2)^6・2C1(1/2)^2 =12(1/2)^8 ・・・③
4回目0・6回目0・8回目0となる確率は、4C4(1/2)^4・2C1(1/2)^2・2C1(1/2)^2 =4(1/2)^8 ・・・④
以上より、求める確率は、①-②-③+④を求めればよい。
解法3.求める確率は、8回目の持ち点が0となる確率から、
4回目0・6回目0以外・8回目0、4回目0以外・6回目0・8回目0、4回目0・6回目0・8回目0となる確率を引けばよい。
8回投げて8回目が0になるのは、表が2回、裏が6回でるときである。
このときの確率は、8C2(1/2)^6・(1/2)^2=8C2(1/2)^8 ・・・①
4回目0・6回目0以外・8回0となる確率は、(1/2)^4・2(1/2)^2・(1/2)^2 =2(1/2)^8 ・・・②
4回目0以外・6回目0・8回0となる確率は、{6C1(1/2)^6ー(1/2)^4・2(1/2)^2}・2(1/2)^2 =2(6C1ー2)・(1/2)^8 ・・・③
4回目0・6回目0・8回0となる確率は、(1/2)^4・2(1/2)^2・2(1/2)^2 =4(1/2)^8 ・・・④
以上より、求める確率は、①-②-③-④を求めればよい。
1.さいころをn個(n≧3)同時に投げるとき、出た目の数の和がn+3になる確率を求めよ。
2.コインを8回投げるゲームをする。最初の持ち点を4点とし、コインを1回投げるごとに、表が出たら持ち点に1点を加え、裏が出たら1点を引く。このとき、ゲーム終了時に、初めて持ち点が0点となる確率を求めよ。

コメントをお書きください