入試問題 · 02/20/2019

国公立大学２次(物理)

大学入試の出題範囲はとても広いので、受験する大学の過去問を10年ほど調べ範囲を絞った上で、出題されそうな分野を中心に勉強します。たとえば、鹿児島大学の物理では、熱力学の出題が多い傾向がありますので、その分野を勉強します。

１．教科書で一通り公式を確認します。

(1) 必須の基本公式

気体状態方程式 $PV = nRT$ 、熱力学第一法則 ${Q_{in}} = \Delta U + {W_{out}}$

(2) 気体の状態変化(定積変化、定圧変化、等温変化、断熱変化)の公式

(A) 定積変化(V＝一定)

P/T＝一定、 ${Q_{in}} = \Delta U$ 　 $({W_{out}} = 0)$ 、 ${Q_{in}} = n{C_v}\Delta T$ 、Cv＝(3/2)R

(B) 定圧変化(P＝一定)

V/T＝一定、 ${W_{out}} = P\Delta V = nR\Delta T,{Q_{in}} = \Delta U + P\Delta V = \Delta U + nR\Delta T$ 、 ${Q_{in}} = n{C_p}\Delta T$ 、Cp＝(5/2)R

PV＝一定 ⇔ ΔT＝０ ⇔ ΔU＝０、 ${Q_{in}} = {W_{out}}$

(D) 断熱変化(Q＝０)

PV/T＝一定、 ${Q_{in}} = 0 \Rightarrow 0 = \Delta U + P\Delta V, P{V^\gamma } = (\gamma = \frac{{{C_p}}}{{{C_v}}} = \frac{5}{3})$

２．過去問を解きます。鹿児島大学(医・獣医など)

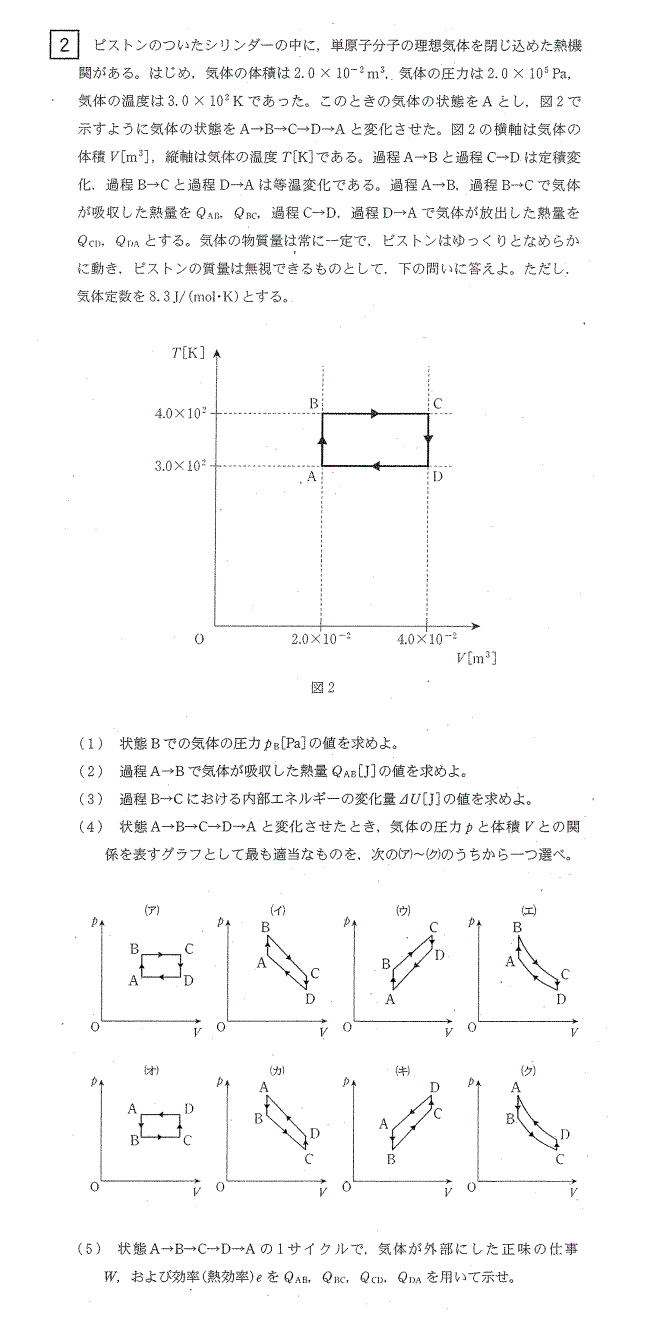
解法のポイント：図２はV-Tグラフであることから、AB間：定積変化、BC間：等温変化、CD間：定積変化、DA間：等温変化、に留意して解きます。

１．公式ボイル・シャルルの法則 PV/T=一定を使います。

PB＝2.7×10^5 [Pa]

２．気体状態方程式 PV＝nTR から、気体の物質量nを求め、定積変化の公式 Qin=nCvΔT で、QABを求めます。

QAB＝2.0×10^3 [J]

３．BC間は等温変化であることから、ΔU＝０となります。

ΔU＝０[J]

４．AB間は定積変化であることから、体積は変化せず、圧力は上昇します。

BC間は等温変化であることから、PV=一定(反比例)のグラフになります。

以上より、答えは(エ)。

５．物体に与えた熱量はQAB, QBCで、物体から放出した熱量はQCD,QDAであることに着目します。

また、A→B→C→D→Aの１サイクルでの内部エネルギーの変化はΔU＝０です。以上より、

外部した仕事は W＝QAB＋QBCーQCD－QDA [J]

物体に与えた熱量はQAB,＋QBCであることより、

熱効率は e ＝(QAB＋QBCーQCD－QDA)/(QAB＋QBC) [J]

３．不明な点を確認して、復習します。

物理は、公式が文字式でそれらが巧妙に絡み合っているので混乱し易く、”覚えるべき原理”と”考えて解くところ”の判別も難しいため、物理に精通した指導者に恵まれるかどうかで学力に大差がついてしまい、映像授業だけで理解不足を解消することは難しい科目です。自分の場合、映像授業などのツールはなくインターネットさえない世代で、指導者もいなかったので、教科書や拙い問題集など、少ない情報の中すべて自力で解決しましたが、習得までにいろいろと遠回りをして苦労しました。そのおかげか、今でも大学入試問題程度なら比較的簡単に解けますが、社会人になって活躍するためには物理に精通した指導者に教わり近道を選び、より高度な学力を身につけた方がよいでしょう。

ちなみに、この入試問題を自力で解いた場合、多くの受験生は(５)に苦戦しますが、熱機関の原理を正しく理解できていればとても簡単な問題です。

カテゴリ：物理

コメントをお書きください

コメント: 0