難関中学2年1学期中間試験の代数の問題(改)です。実際には代数と幾何の融合問題になっていて、解の公式、相似など公立中では3年で履修する単元を含んでいます。この問題の難易度は慶應高入試レベルですが、小学生のとき、多くが遊んでいる間に必死で難問と格闘し磨き上げた学力のおかげで、この学校の生徒たちは中学入学後1年程度の学習で解けるようになります。公立高入試向けの勉強しかしていないと解けませんが、このような難問に挑戦し続けると解けるようになり、一気に学力が上がります。東大の問題も、難度が少し低い横国大や傾向が大きく異なる早慶大の問題しか解いたことがないと、大苦戦しますが、東大・京大の類問に挑戦し続けると自然と解けるようになるのと同じです。
このレベルの問題は公立高校入試には出題されません。以前、長野県がこれより少し易しい問題を出題したことがありますが、それでも難度の高さにショックを受けてトップ高をはじめとして合格するはずの多くの生徒が受験に失敗し、大問題になったことがあります。以後、公立高入試では難問は出題されていません。部活を続けてもまじめにコツコツ勉強すれば誰でもトップ校に合格できることを前提に公立高校の入試問題は作成されるのが一般的ですから、長野で大問題になったのは当然です。ただし、私立高や大学の入試では、このような制約はありません。
大学入試はどこであっても”難問を出してはいけないという制約”はないので、学校の定期試験で高得点をとってもまたトップ高生であっても、油断していると呆気ないほど簡単に落ちます。部活に熱中しながらコツコツ勉強し公立進学校に合格した成功体験は、大学受験ではまったく通用しません。大学入試では中堅大学でさえ、(公立トップ校であっても)学校では未習の問題が頻出ですから、合格するには学校外でより広くより深く学習することが必須です。
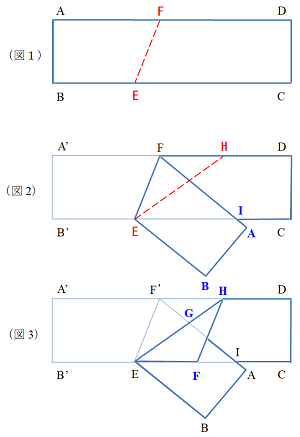
(図1)において、長方形ABCDの紙をEFで折る。
ここで、(図1)のA,Bの点を(図2)ではそれぞれA’,B’とし、FAとB’Cとの交点をIとする。
(図2)において、FがEI上にあるように、EHで折る。
ここで、(図2)のFを(図3)ではF’とし、(図3)のF’IとEHとの交点をGとする。
(図3)においてGE=GI、AF’=1であるとき、次の問いに答えよ。
(1) (図3)の∠EF’Gの角度を求めよ。
(2) (図3)のEF’の長さを求めよ。
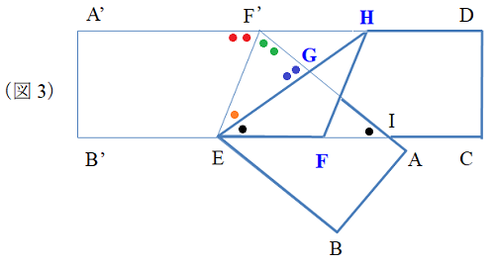
(1) GE=GIより△GEIは二等辺三角形であるから、
∠GEI = a とおくと
∠GEI=∠EIG=a、∠EGF’=2a ・・・➀
(黒●、黒●、青●●)
EHに関して線対称であるから、
△EFH ≡△EF’H ・・・②
②より∠GEF=∠GEF’=a 、∠F’EF = 2a ・・・③
(黒●、オレンジ●、黒オレンジ●●)
A’D//BC’より、∠F’EF=∠EF’A’= 2a ・・・④
(黒オレンジ●●、赤●●)
EF’に関して線対称であるから、
四角形EBAF’≡四角形EB’A’F’ ・・・⑤
④,⑤より、∠EF’A’=∠EF’G=2a ・・・⑥
(赤●●、緑●●)
➀,③,⑥より、
△EF’Gにおいて∠E=a, ∠F’=2a, ∠G=2a であるから、
a+2a+2a=180°⇔ a = 72°∴∠EF’G=72°
(2)△IF’Eと△EF’Gにおいて、
(1)の➀~⑥より∠IEF’=∠IF’E = ∠EF’G=∠EGF’であるから、
△IEF’ ∽ △EF’G
EF’=x とおくと、IG=EG=EF’=x , IF’:F’E = EF’:F’G=1:x であるから、
IF’ = 1, IG = x , G F’=x2である。よって、
x2+x=1 これを解くと
,
x >
0 より、EF=

コメントをお書きください